1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
|
from ast import parse, NodeVisitor, Name
_NAMES = {
'Add': '+',
'And': 'and',
'Assert': 'assert',
'Assign': '=',
'AugAssign': 'op=',
'BitAnd': '&',
'BitOr': '|',
'BitXor': '^',
'Break': 'break',
'Recursion': 'recursive call',
'ClassDef': 'class',
'Continue': 'continue',
'Del': 'del',
'Delete': 'delete',
'Dict': '{...}',
'DictComp': '{...}',
'Div': '/',
'Ellipsis': '...',
'Eq': '==',
'ExceptHandler': 'except',
'ExtSlice': '[::]',
'FloorDiv': '//',
'For': 'for',
'FunctionDef': 'def',
'GeneratorExp': '(... for ...)',
'Global': 'global',
'Gt': '>',
'GtE': '>=',
'If': 'if',
'IfExp': '...if...else...',
'Import': 'import',
'ImportFrom': 'from ... import ...',
'In': 'in',
'Index': '...[...]',
'Invert': '~',
'Is': 'is',
'IsNot': 'is not ',
'LShift': '<<',
'Lambda': 'lambda',
'List': '[...]',
'ListComp': '[...for...]',
'Lt': '<',
'LtE': '<=',
'Mod': '%',
'Mult': '*',
'Nonlocal': 'nonlocal',
'Not': 'not',
'NotEq': '!=',
'NotIn': 'not in',
'Or': 'or',
'Pass': 'pass',
'Pow': '**',
'RShift': '>>',
'Raise': 'raise',
'Return': 'return',
'Set': '{ ... } (set)',
'SetComp': '{ ... for ... } (set)',
'Slice': '[ : ]',
'Starred': '',
'Sub': '-',
'Subscript': '[]',
'Try': 'try',
'Tuple': '(... , ... )',
'UAdd': '+',
'USub': '-',
'While': 'while',
'With': 'with',
'Yield': 'yield',
'YieldFrom': 'yield from',
}
def check(source_file, checked_funcs, disallow, source=None):
"""Checks that AST nodes whose type names are present in DISALLOW
(an object supporting 'in') are not present in the function(s) named
CHECKED_FUNCS in SOURCE. By default, SOURCE is the contents of the
file SOURCE_FILE. CHECKED_FUNCS is either a string (indicating a single
name) or an object of some other type that supports 'in'. CHECKED_FUNCS
may contain __main__ to indicate an entire module. Prints reports of
each prohibited node and returns True iff none are found.
See ast.__dir__() for AST type names. The special node name 'Recursion'
checks for overtly recursive calls (i.e., calls of the form NAME(...) where
NAME is an enclosing def."""
return ExclusionChecker(disallow).check(source_file, checked_funcs, source)
class ExclusionChecker(NodeVisitor):
"""An AST visitor that checks that certain constructs are excluded from
parts of a program. ExclusionChecker(EXC) checks that AST node types
whose names are in the sequence or set EXC are not present. Its check
method visits nodes in a given function of a source file checking that the
indicated node types are not used."""
def __init__(self, disallow=()):
"""DISALLOW is the initial default list of disallowed
node-type names."""
self._disallow = set(disallow)
self._checking = False
self._errs = 0
def generic_visit(self, node):
if self._checking and type(node).__name__ in self._disallow:
self._report(node)
super().generic_visit(node)
def visit_Module(self, node):
if "__main__" in self._checked_funcs:
self._checking = True
self._checked_name = self._source_file
super().generic_visit(node)
def visit_Call(self, node):
if 'Recursion' in self._disallow and \
type(node.func) is Name and \
node.func.id in self._func_nest:
self._report(node, "should not be recursive")
self.generic_visit(node)
def visit_FunctionDef(self, node):
self._func_nest.append(node.name)
if self._checking:
self.generic_visit(node)
elif node.name in self._checked_funcs:
self._checked_name = "Function " + node.name
checking0 = self._checking
self._checking = True
super().generic_visit(node)
self._checking = checking0
self._func_nest.pop()
def _report(self, node, msg=None):
node_name = _NAMES.get(type(node).__name__, type(node).__name__)
if msg is None:
msg = "should not contain '{}'".format(node_name)
print("{} {}".format(self._checked_name, msg))
self._errs += 1
def errors(self):
"""Returns the number of number of prohibited constructs found in
the last call to check."""
return self._errs
def check(self, source_file, checked_funcs, disallow=None, source=None):
"""Checks that AST nodes whose type names are present in DISALLOW
(an object supporting the contains test) are not present in
the function(s) named CHECKED_FUNCS in SOURCE. By default, SOURCE
is the contents of the file SOURCE_FILE. DISALLOW defaults to the
argument given to the constructor (and resets that value if it is
present). CHECKED_FUNCS is either a string (indicating a single
name) or an object of some other type that supports 'in'.
CHECKED_FUNCS may contain __main__ to indicate an entire module.
Prints reports of each prohibited node and returns True iff none
are found.
See ast.__dir__() for AST type names. The special node name
'Recursion' checks for overtly recursive calls (i.e., calls of the
form NAME(...) where NAME is an enclosing def."""
self._checking = False
self._source_file = source_file
self._func_nest = []
if type(checked_funcs) is str:
self._checked_funcs = { checked_funcs }
else:
self._checked_funcs = set(checked_funcs)
if disallow is not None:
self._disallow = set(disallow)
if source is None:
with open(source_file) as inp:
p = parse(open(source_file).read(), source_file)
else:
p = parse(source, source_file)
self._errs = 0
self.visit(p)
return self._errs == 0
|


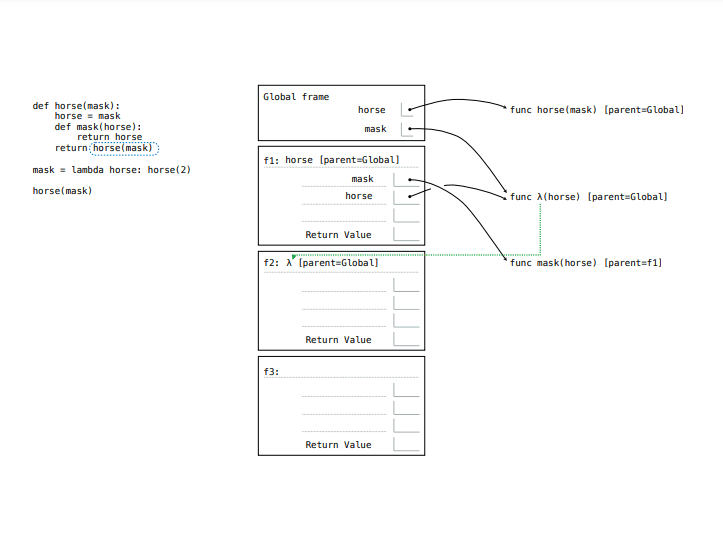

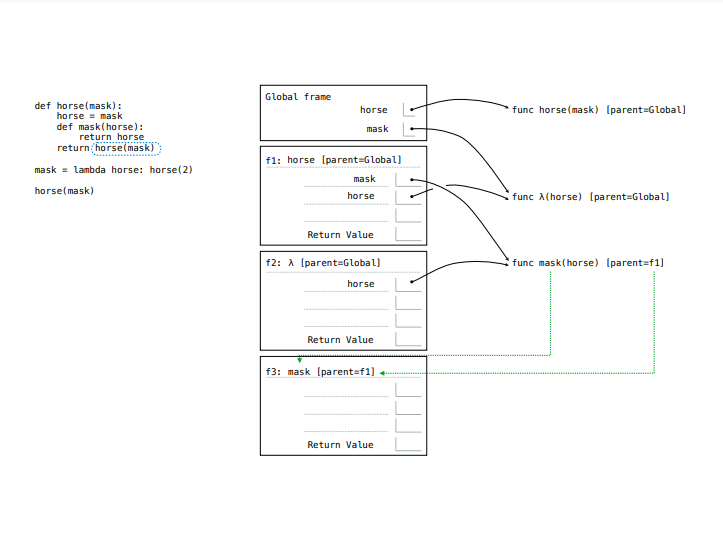
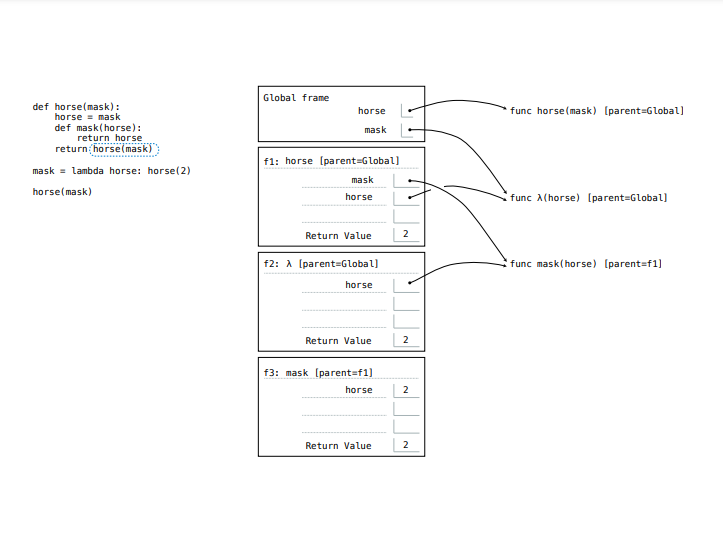
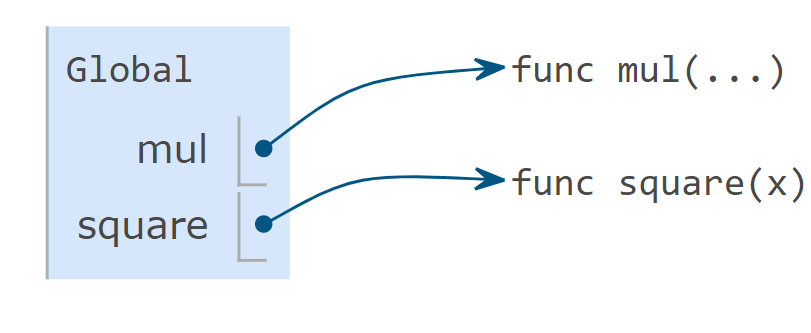


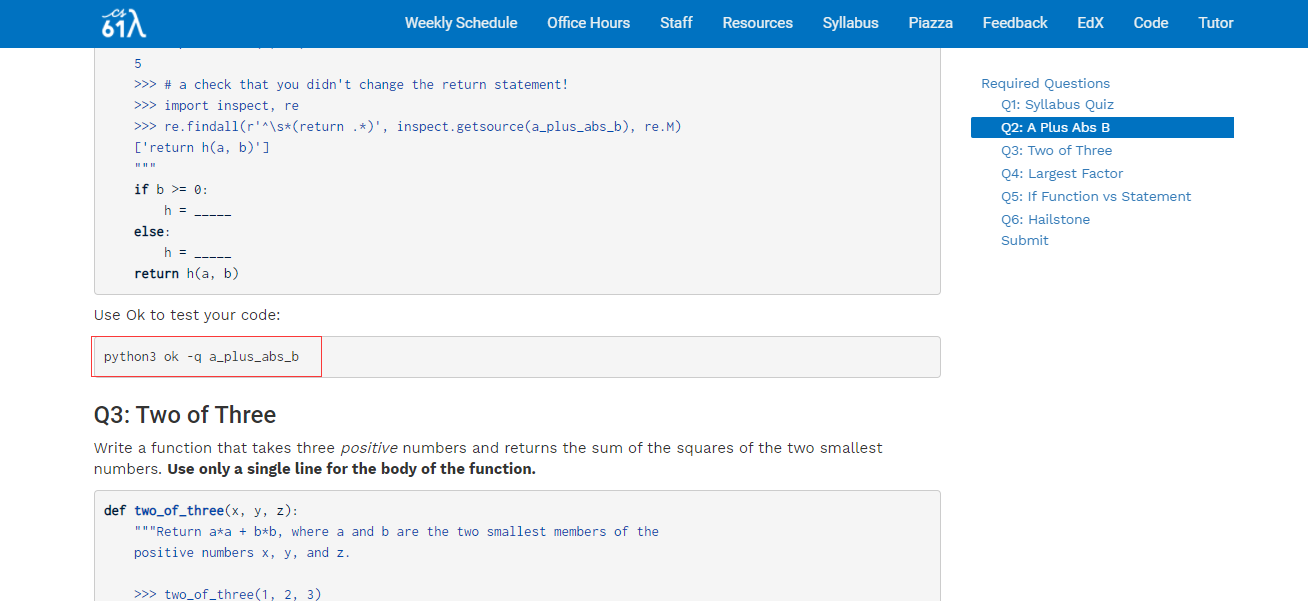
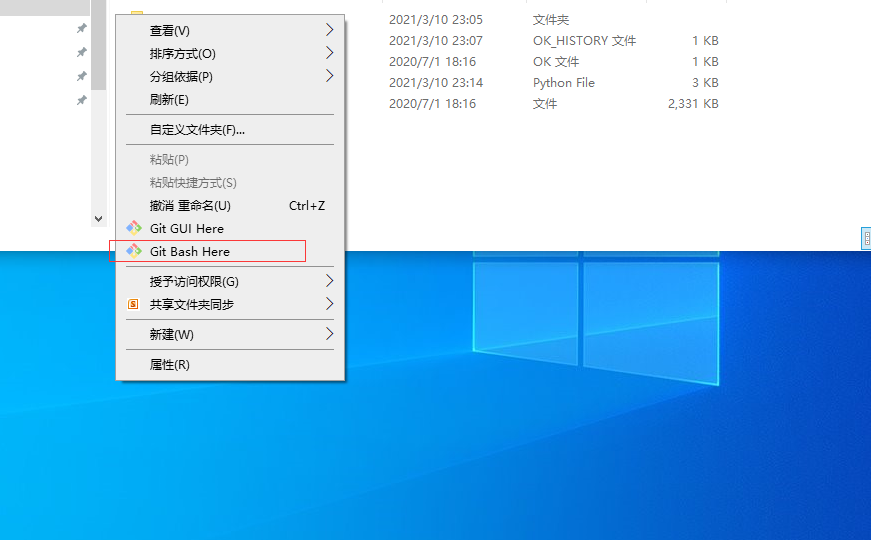
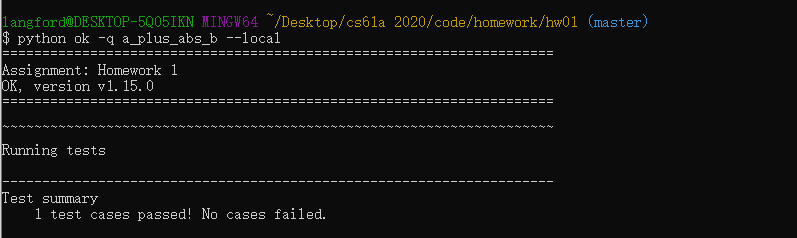
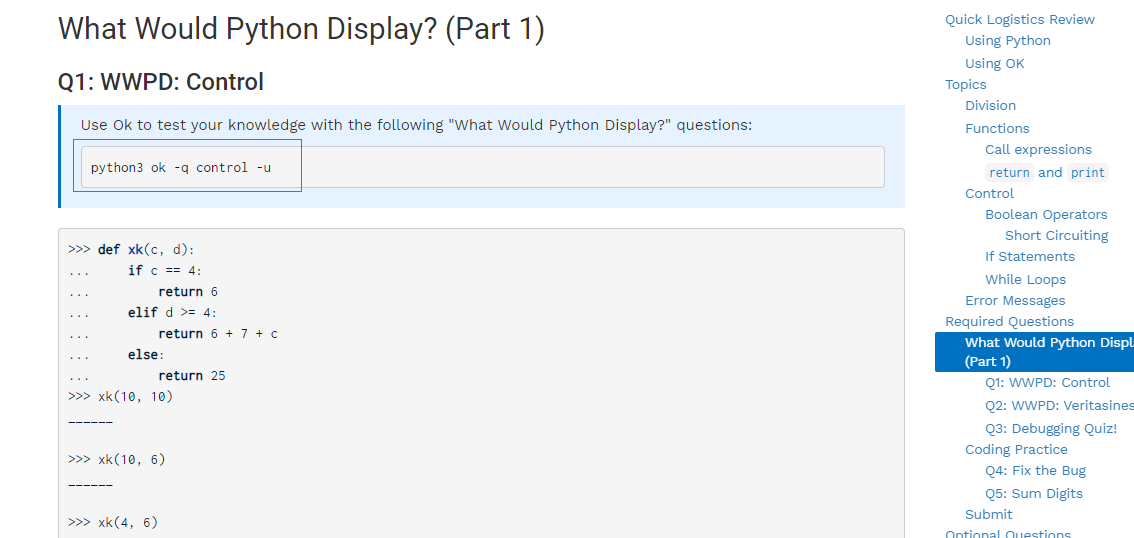
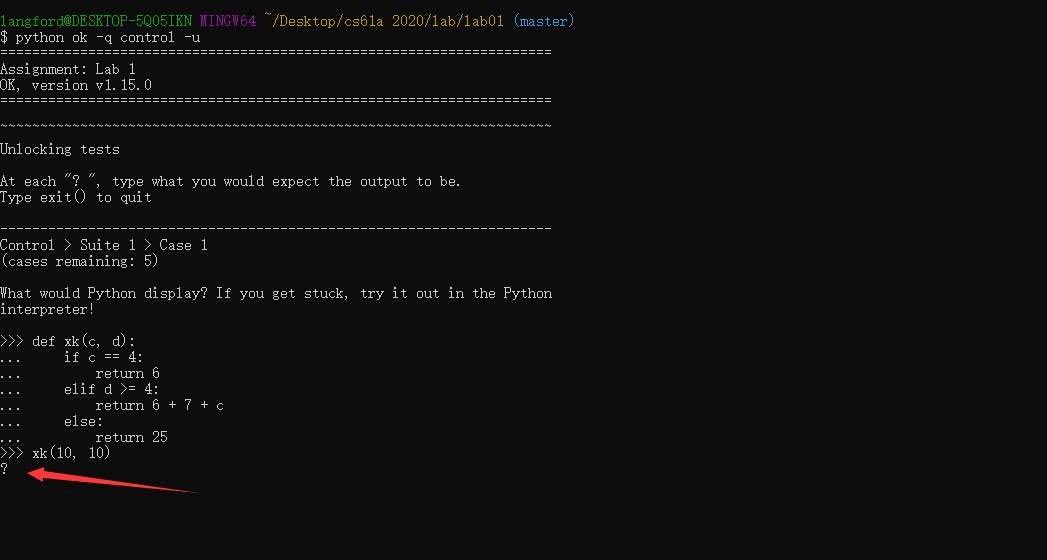
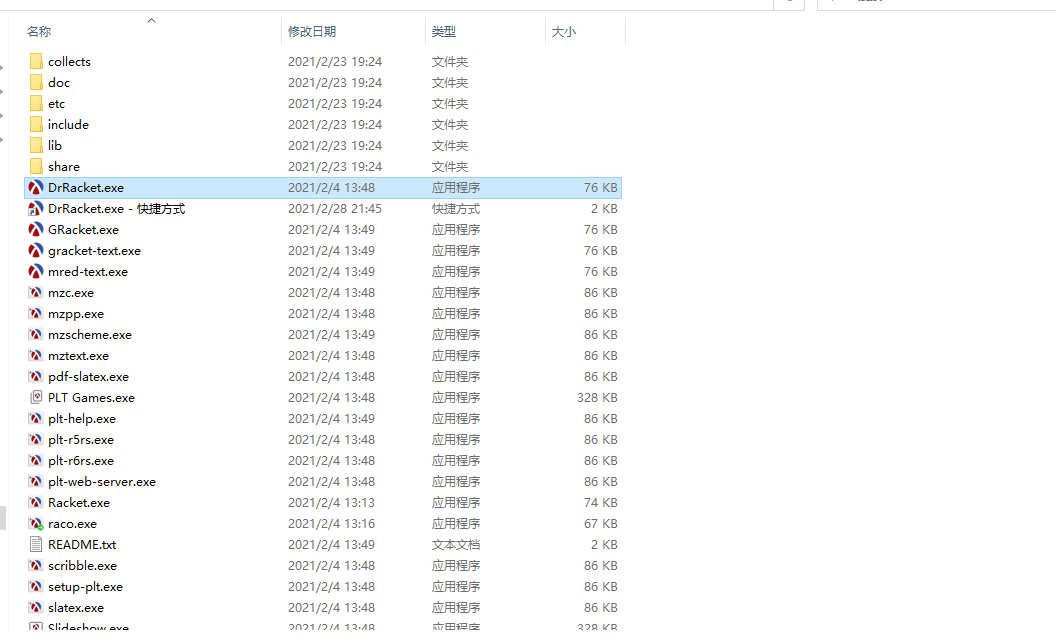 打开,看到所示页面
打开,看到所示页面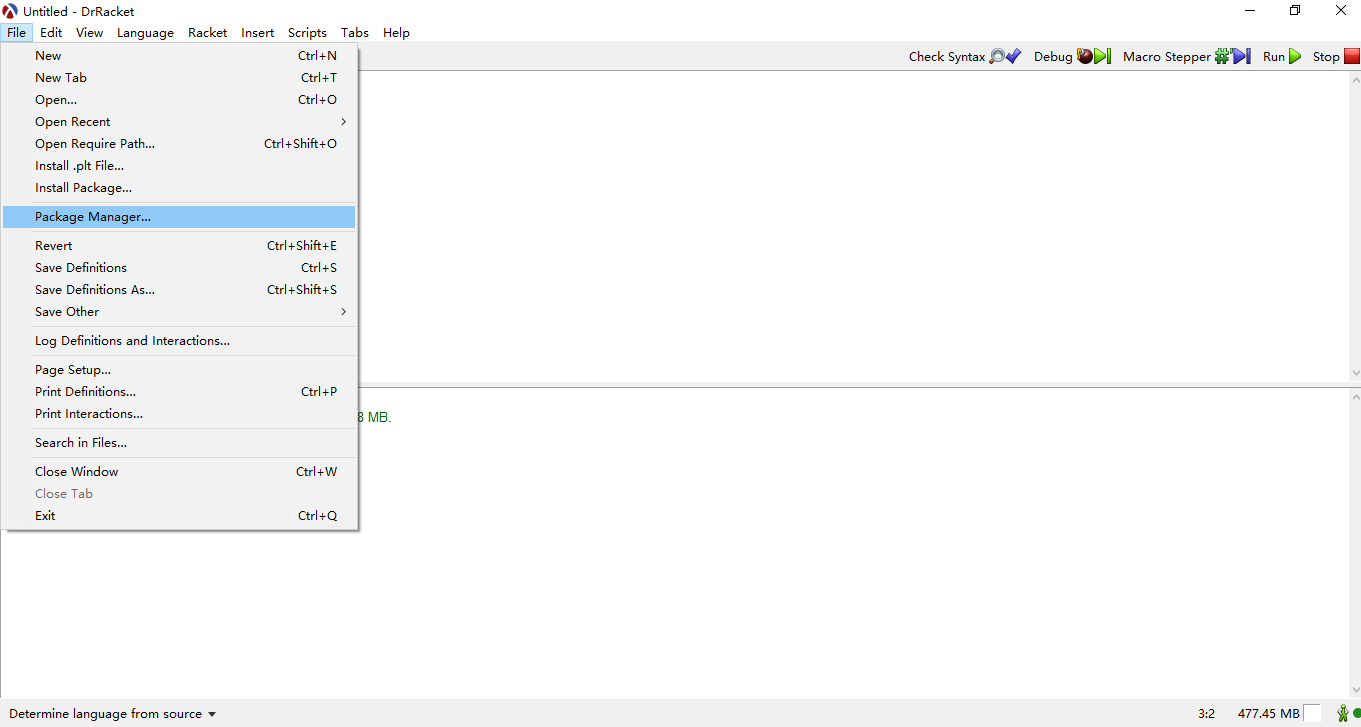 点击package manager,在这里我们有两种选择,都同样的可以满足本课程的全部所需,见下图
点击package manager,在这里我们有两种选择,都同样的可以满足本课程的全部所需,见下图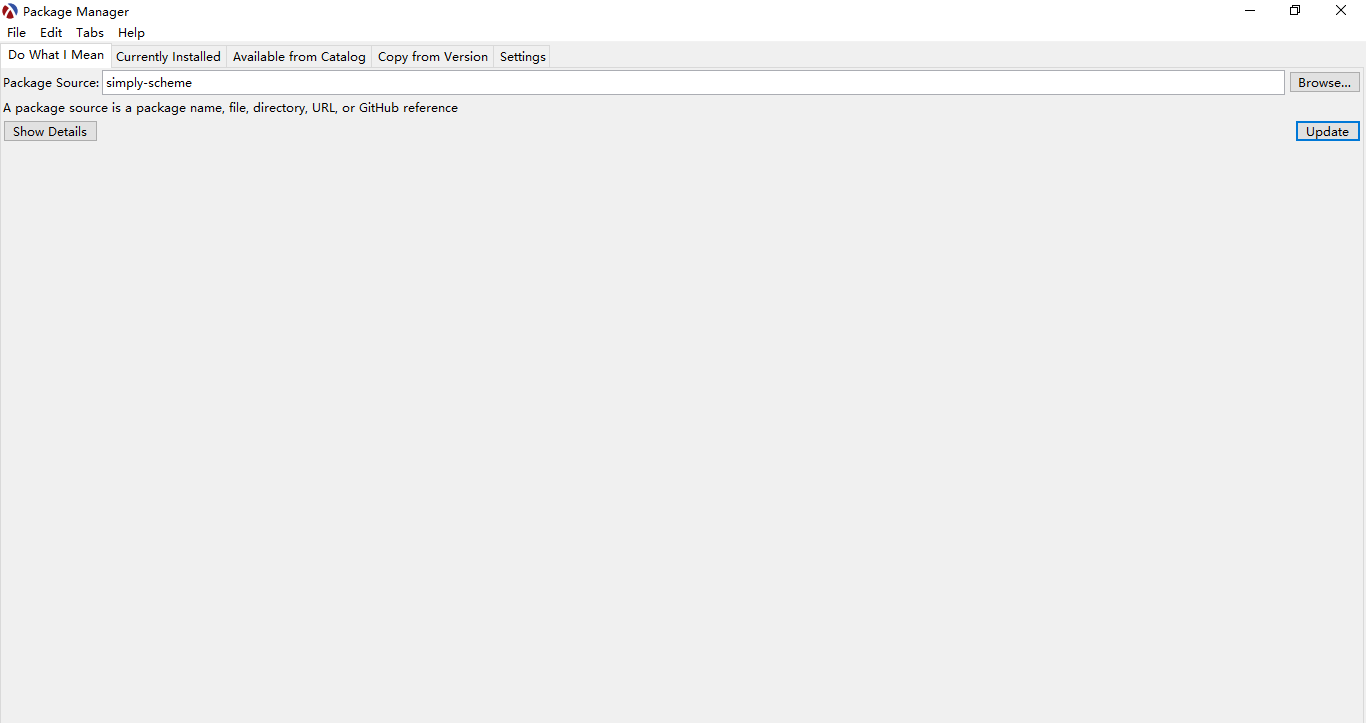
 点击下载即可。进入DrRacket后你会发现界面分为两个部分,上面的部分是我们需要输入代码的区域,而下半部分则是输出反馈。
点击下载即可。进入DrRacket后你会发现界面分为两个部分,上面的部分是我们需要输入代码的区域,而下半部分则是输出反馈。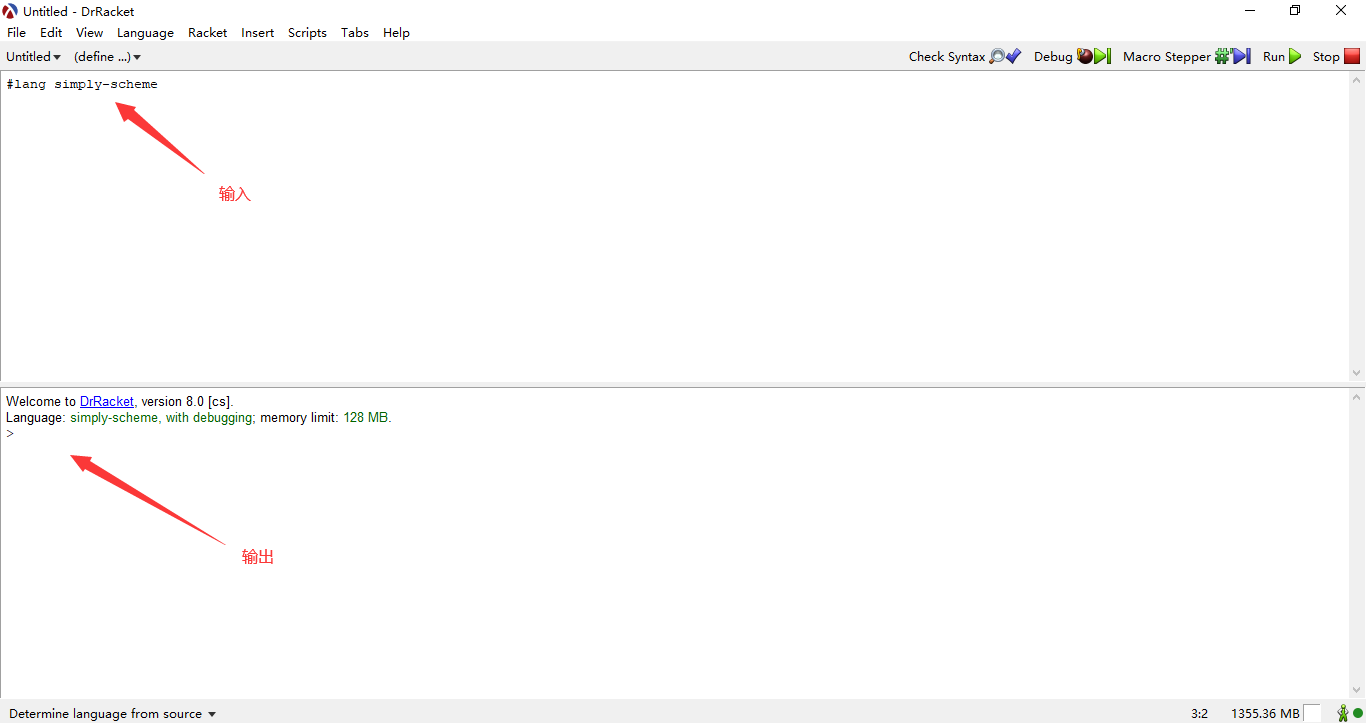
 若无,则有可能出现编译错误或者自己在写程序时忘记添加语言选择。
若无,则有可能出现编译错误或者自己在写程序时忘记添加语言选择。 ![sec函数图像,引自[2]](/2021/02/19/%E9%AB%98%E7%AD%89%E6%95%B0%E5%AD%A61/sec.png)
![三角函数关系,引自[3]](/2021/02/19/%E9%AB%98%E7%AD%89%E6%95%B0%E5%AD%A61/hexagon.jpg)


![Local vcs示意图,引自[3]](/2021/02/04/Git-and-Github/Lvcs.png)
![Centralized vcs示意图,引自[3]](/2021/02/04/Git-and-Github/Cvcs.png) Distributed VCS填补了这样的问题。
Distributed VCS填补了这样的问题。![Distributed vcs示意图,引自[3]](/2021/02/04/Git-and-Github/Dvcs.png) Git就是帮助我们实现这一切的软件,而我们使用Git上传到的数据中心,就是大名鼎鼎的Github。
Git就是帮助我们实现这一切的软件,而我们使用Git上传到的数据中心,就是大名鼎鼎的Github。
